【05-11】力扣每日一题

白羽发间插，流星腰后挂。

常怀报国志，何处不为家。

题目内容

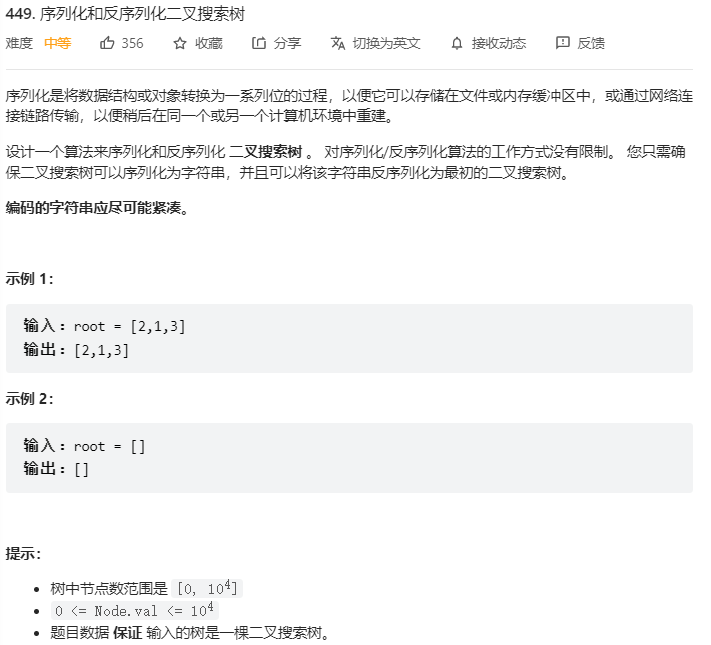
题目分析

这道题目比较贴近我们日常的应用，是关于序列化和反序列化的问题。题目的意思，简单来说就是，给你一个二叉搜索树，你需要将其序列化成字符串，并且序列化成字符串之后，从字符串能够反序列化成这个二叉搜索树的结构。

想到这里，我想起以前做过的一道题目，给你前序遍历和中序遍历的结果或者给你后序遍历和中序遍历的结果，你来还原二叉树的结构。那么这里同样可以这样做，我们选用中序遍历+后序遍历的组合。因为二叉搜索树的中序遍历的结果就是从小到大的升序排序结果。所以对于序列化的方法，我们只需要将二叉树进行后序遍历，得到后序遍历的结果即可。然后对于反序列化，我们首先将后序遍历的结果排序（按照升序的方式排），那么不就得到了中序遍历的结果，之后结合原来的后续遍历即可实现二叉搜索树的构建。当然这个题目我们可以不用排序，直接根据二叉搜索树的特点直接写代码，看下面的代码就懂了。

这里对于使用中序+后序构建二叉搜索树，这里简单说一下，我们使用栈的数据结构来帮助我们完成。我们知道中序遍历的方式是左根右，而后续遍历的方式是左右根，那么对于后序遍历而言其末尾就是我们的根节点。

代码实现

c++代码实现如下：

class Codec {
public:
    string serialize(TreeNode* root) {
        string res;
        vector<int> arr;
        // 后序遍历 遍历结果放在数组arr里
        postOrder(root, arr);
        if (arr.size() == 0) {
            // 根节点为空 直接返回空字符串
            return res;
        }
        for (int i = 0; i < arr.size() - 1; i++) {
            // 每个结点的值使用逗号隔开
            res.append(to_string(arr[i]) + ",");
        }
        res.append(to_string(arr.back()));
        return res;
    }

    vector<string> split(const string &str, char dec) {
        int pos = 0;
        int start = 0;
        vector<string> res;
        // 分隔开每一个逗号
        while (pos < str.size()) {
            while (pos < str.size() && str[pos] == dec) {
                pos++;
            }
            // 非逗号起点
            start = pos;
            while (pos < str.size() && str[pos] != dec) {
                pos++;
            }
            // 此时的pos为逗号终点
            if (start < str.size()) {
                res.emplace_back(str.substr(start, pos - start));
            }
        }
        return res;
    }

    TreeNode* deserialize(string data) {
        if (data.size() == 0) {
            return nullptr;
        }
        vector<string> arr = split(data, ',');
        stack<int> st;
        // 栈放后序遍历的结果
        for (auto & str : arr) {
            st.emplace(stoi(str));
        }
        return construct(INT_MIN, INT_MAX, st);
    }

    void postOrder(TreeNode *root,vector<int> & arr) {
        if (root == nullptr) {
            // 结点为空指针 直接返回
            return;
        }
        // 先遍历左子树
        postOrder(root->left, arr);
        // 然后遍历右子树
        postOrder(root->right, arr);
        // 最后访问根节点
        arr.emplace_back(root->val);
    }

    TreeNode * construct(int lower, int upper, stack<int> & st) {
        if (st.size() == 0 || st.top() < lower || st.top() > upper) {
            // 当栈为空 或者 数据不符合要求 返回空指针
            return nullptr;
        }
        int val = st.top();
        st.pop();
        // 因为后序遍历是 左右根 所以从后往前 是 根右左
        TreeNode *root = new TreeNode(val);
        // 构建右子树 因为是二叉搜索树 所以 右子树最小值为 val
        root->right = construct(val, upper, st);
        // 构建左子树 因为是二叉搜索树
        root->left = construct(lower, val, st);
        return root;
    }
};