NeRF-用于视角合成的神经辐射场

文章解读

整体介绍

首先，简单介绍一下NeRF是怎么做的。在NeRF中，输入是位置信息以及两个角度信息，对于位置信息我们很容易理解就是空间中点的坐标，其中θ和φ就是球面坐标中的θ和φ，如下图所示，这个很容易理解。

那么也就是输入空间点的坐标以及对应的角度信息，那么如何获取空间点的坐标和角度信息呢？首先我们有不同视角的图像，也就是我们从空间中不同位置处拍摄了图像，以相机位置为光源，连接光源和图像中每一个像素，这样就得到我们的射线，将射线延长并在[near,far]的范围内每隔t进行采样，这样就得到了采样的点的坐标。对于方向，我们知道3维空间中方向向量的表示和点是一样的，也是(x,y,z)。那么现在通过这样一系列操作之后我们能够得到n张图像的采样点以及对应的方向向量，之后需要输入到网络中预测每个点的颜色和体积密度(可以简单理解为不透明度)。一旦训练完成，该场景中每个点的颜色和体积密度是确定的，那么一旦给定视角，从这个视角发射光线采样点，就能够得到一条光线上每个点的颜色和体积密度，之后将一条光线上点的颜色和体积密度进行积分就得到图像中某个像素点的颜色了。

对于NeRF中loss的计算也很好理解，它使用的是2D图像对其进行监督（求mse loss）。首先NeRF输入的采样点是根据每一张图像发射光线采样得到的，那么在训练的过程中，我们是想网络能够对某个点坐标以及带有对应的方向信息预测颜色(color)以及体积密度(density)。一旦网络能够给出颜色和体积密度，那么我们按照输入的光线进行积分，那么就能够得到对应的图像，将渲染得到的图像与真实的图像做mse loss，这样便实现网络的训练。

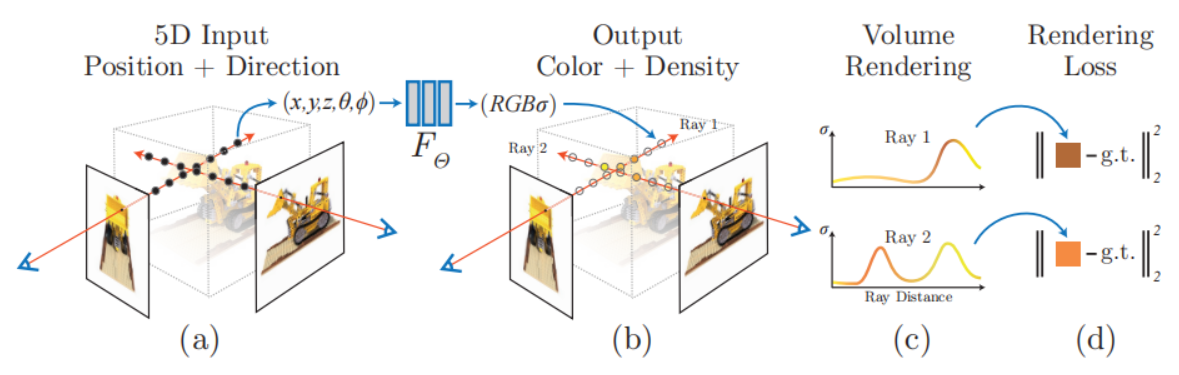
所以NeRF训练的整体过程可以概括如下：

首先根据相机的位姿生成对应的光线。
根据光线采样对应的点，光线模型: p = rays_o + t * rays_d (p是点坐标，rays_o是光源，rays_d是方向向量，t是采样的距离)
将点和角度进行编码，文中实验表明，将坐标和方向进行编码能够更好地表现高频信息。
将编码后的向量输入模型，进行预测，预测得到的结果渲染成相应的图像与真实图像做loss

NeRF本身使用的网络结构也非常简单，如下图所示，前8层就是普通的全连接网络，并且在第5层的时候输入位置编码的信息形成残差结构，在第9层的时候有一个256到1的全连接，预测得到体积密度，接着后面的128个单元的线性层映射RGB。

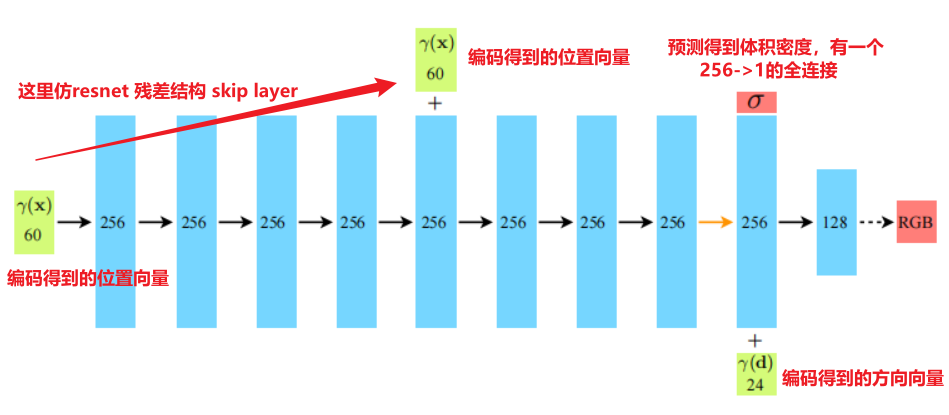
NeRF的思想其实是借鉴的物理学的相关知识，人眼能够看到颜色是因为光照射到物体当中物体选择性的吸收了一些颜色的光，剩下颜色的光通过反射到达人眼，人眼的感觉细胞刺激大脑中枢，从而产生颜色感觉。在NeRF中通过对场景进行建模，某个像素点最终的颜色体现在相机中心与像素点连线形成的射线上面的点的颜色进行积分，产生最后的颜色。同时使用体积密度的概念来表示透射率，从而对物体吸收光线做出建模。总结一下NeRF的优缺点如下：

能够逼真的进行场景重建（重建出来的效果和比传统的更加逼真），而且这种场景是隐式的重建。
- 通常来说3D的显示表示主要有：深度图(depth map)、点云(point cloud)、体素(voxel)、网格(mesh)。而NeRF中的隐式表示指的是用神经网络隐式表示了3D场景，不能够显示表示。不过通过NeRF也能够拿到深度图以及mesh，这些放在后面来说。
能够根据已知的少量图像渲染出任意视角的图像，举个例子，假设我们的输入是绕一个物体每隔4°拍一张照片，那么绕物体一圈就能够拿到90张照片。然后我们使用NeRF进行场景重建，之后便能够渲染出任意一个视角的图像（比如说0°和4°我们都见过，现在渲染视角为3°的照片）
虽然说NeRF是隐式重建，题目中说了是为了渲染新视角的图像的。不过NeRF也可以拿到显示模型，比如说mesh，在NeRF原作者的代码里提供了一种显式化的方式，也就是利用得到的体积密度使用Marching Cubes的方式来提取mesh，从而实现模型的显式化。
当然说完NeRF也有缺点，其缺点如下。
- 一次训练就是一次重建，训练完的模型只能够用于该场景不能用于其它场景。
- 一次训练耗时较长(100k-300k的迭代次数在单张V100需要耗费1-2天)，测试的时候渲染图像也比较耗时（单张V100大概30秒渲染一张图像）。
- 只能够重建静态场景，也就是要求场景中不能够有动态的物体。
- 对输入图像的数目要求较多，在NeRF原文中呈现的这个lego car，大概需要100张图像重建，并且每一张图像拍摄的位置距离物体是在一定范围内的，不能过近或者过远。
- 重建的好坏依赖于图像数目以及位姿的准确性，如果你想使用自己拍摄的数据进行重建，那么需要使用colmap等工具来计算相机位姿，相机位姿的准确度高低决定着你重建质量的高低。

以上就是对NeRF的整体介绍，接下来我们需要详细去推导，理解其原理了，搞明白NeRF为什么能行。

公式推导和原理分析

在讲公式推导之前，我们先列出以下几个概念，方便之后公式推导的理解：

密度场 $\sigma(x)$ ，其中x表示空间中某一点，密度场则表示射线撞击粒子的微分似然度，换句话说也就是射线在行进无穷小距离时撞击粒子的概率（假设在世界空间里，物体是由粒子组成的）。
透射率 $\Tau(t)$ ，表示光线在[0,t)上传播而没有击中任何粒子的概率。而t表示的是沿着光线方向光线行进的步长。对于射线，我们通常使用 $r(o,d)$ 表示，因为沿着射线(光线)的任意点都可以写成 $r(t) = o+td$ ，表示从光源o，沿着方向d行进t的步长。所以透射率中的t表示的是步长。
累计分布函数(CDF)和概率密度(PDF)，我们知道，在概率论中有CDF和PDF，其中PDF是CDF导数，CDF是PDF的积分。

首先我们先来推导一下透射率的公式，透射率 $\tau(t)$ 表示光线在[0,t)范围内传播而没有击中任何东西的概率，那么当行进 $dt$ 步长的时候， $\Tau(t+dt)$ 表示在[0,t+dt)范围内传播而没有击中任何东西的概率，等价于在[0,t)上没有击中任何东西的概率乘以在[t,t+dt)上没有击中任何东西的概率也即是 $\Tau(t+dt) = \Tau(t)(1 - dt\cdot\sigma(t))$ ，因为dt很小，所以t+dt这一段区域的密度场可以看做是t位置时的密度场，而密度场表示物体撞击粒子的概率，那么 $dt\cdot\sigma(t)$ 就表示[t,t+dt)这一段区间内撞击粒子的概率，然后用1减去这个概率就是这一段区间[t,t+dt)没有撞击到粒子的概率。接下来就是利用这个等式进行推导，推导过程如下：

\Tau(t + dt) = \Tau(t)(1 - dt\cdot\sigma(t))

\Tau(t+dt) = \Tau(t) - \Tau(t)\cdot dt\cdot \sigma(t)

\frac{\Tau(t+dt) - \Tau(t)}{dt} = -\Tau(t) \cdot \sigma(t)

\Tau^{'}(t) = -\Tau(t) \cdot \sigma(t)

\frac{\Tau^{'}(t)}{\Tau(t)} = -\sigma(t)

\int_{a}^{b} \frac{\Tau^{'}(t)}{\Tau(t)}dt = -\int_{a}^{b} \sigma(t)dt

\log \Tau(t)|_{a}^{b} = -\int_{a}^{b} \sigma(t)dt

\Tau(b) - \Tau(a) = exp(-\int_{a}^{b} \sigma(t)dt)

公式1就是我们原来的等式，公式2、3、4、5就是普通的恒等变换，公式6这里就对左右进行一个积分，一直到公式8。我们知道 $\Tau(t)$ 表示光线在[0,t)上传播而没有碰到任何粒子的概率。最后得到的公式8表示的是光线从[a,b)没有碰到任何粒子的概率，这个公式也就对应着NeRF原文中section 4里的公式1里的 $\Tau(t)$ 了。根据 $\Tau(t)$ 的含义，我们知道 $1 - \Tau(t)$ 表示的是不透明度，表示光线确实在到达t之前撞击粒子的概率。而 $\Tau(t)\sigma(t)$ 表示光线在[0,t)传播没有撞到粒子的概率乘以刚好在t处撞到粒子的概率，等于光线在[0,t]处传播最终刚好在t处停下的概率。所以 $\Tau(t)\sigma(t)$ 表示PDF，不透明度表示的是CDF。

推导完透射率函数之后我们来推导一下体积渲染的公式。现在我们可以计算光线从t=0传播到D时体积中的粒子发出的光的预期值，并且合成在背景颜色之上。而目前在t处停止的概率密度为 $\Tau(t)\cdot\sigma(t)$ ，那么预期的颜色如公式9所示，首先从0到D积分表示从0到D采样，而前两项表示在t处停止的概率那么自然要乘以对应的颜色c(t)，并且积分。同时也要加上在D处背景颜色，其中 $c_{bg}$ 是根据残差透射率 $\Tau(D)$ 与前景合成的背景色，不失一般性，在下文中我们省略了背景术语。

C = \int_{0}^{D}\Tau(t)\cdot \sigma(t)\cdot c(t)dt + \Tau(D)\cdot c_{bg}

至此我们推导出原文给出的第一个公式，如下图所示。其中的 $\Tau(t)$ 就是我们最开始推导的透射率，而这个积分公式和我们推导的公式9别无二致。

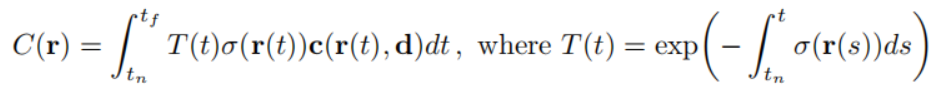
接下来我们需要讨论一下同质媒体，同质媒体也就是在一定范围内[a,b]具有恒定颜色 $c_{a}$ 和体积密度 $\sigma_{a}$ 。那么光线从a到b经过同质媒体渲染出来的颜色是什么样的呢？我们看下面的推导。

\bold{C}(a \rightarrow b) = \int_{a}^{b} \Tau(a \rightarrow t)\cdot \sigma(t) \cdot c(t)dt

= \sigma_{a} \cdot c_{a}\int_{a}^{b} \Tau(a \rightarrow t)dt

= \sigma_{a} \cdot c_{a} \int_{a}^{b}exp(-\int_{a}^{t}\sigma(u)du)dt

= \sigma_{a} \cdot c_{a} \int_{a}^{b}exp(-\sigma_{a}u|_{a}^{t})dt

= \sigma_{a} \cdot c_{a} \int_{a}^{b}exp(-\sigma_{a}(t-a))dt

= \sigma_{a} \cdot c_{a} \frac{exp(-\sigma_{a}(t-a))}{-\sigma_{a}}|_{a}^{b}

= c_{a} \cdot (1 - exp(-\sigma_{a}(b-a)))

首先公式10是我们需要计算的光线从a到b之后经过同质媒体渲染出来的颜色，公式11是因为同质媒体的原因直接代入常数，公式12是等价代换透射率的公式，公式13就是普通的定积分，公式14是写成相减的形式，公式15也是求定积分得到公式16。而在NeRF原文中，作者说明采样的范围为 $[t_{n},t_{f}]$ ，在这个范围内均匀采样，那么每一段就是 $\frac{t_{f} - t_{n}}{N}$ ，总共有N段，那么每一段的起点和终点公式17所示。这也是论文原文的公式2。

[t_{n}+\frac{i-1}{N}(t_{f} - t_{n}),t_{n}+\frac{i}{N}(t_{f} - t_{n})]

积分形式通常在计算机中表示为求和，按照上面的分段策略，我们可以推导出NeRF原文的公式3，如下图所示，其中 $\delta_{i} = t_{i+1} - t_{i}$ ，这个公式我没有直接推导，但是对照我们推导的公式9和公式16可以很容易写出积分的离散形式。至此公式推导结束。

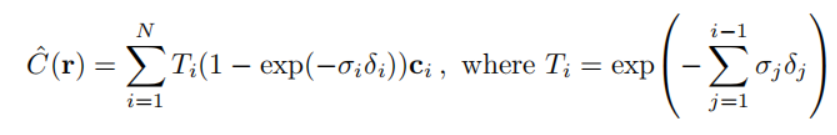
接下来我们来聊聊，NeRF中的一些其它的细节。首先是位置编码，如下所示。作者认为，神经网络只能够学习到一些低频特征，而对于那些高频特征则学习不到。为了使网络能够学习到高频特征，作者将输入的位置和方向进行编码，对于位置，进行10次编码取得高频特征，而每次编码会得到正弦编码和余弦编码，所以每次得到的向量cat之后为6，10次就是60。而方向上作者进行了4次编码，也就是24维度的向量。

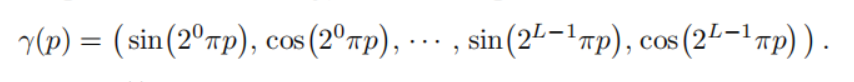
有编码和没有编码在效果上的区别如下图所示，可以很明显的看到有位置编码的能够明显表现出高频特征。

另外一个优化的方式就是分层体素采样，我们可以想像到，在一个空间中采样，会采到很多没用的点，或者不是物体上的点。使得模型无法很好地收敛。于是作者采用一个粗到细的方式进行分层采样，首先有一个coarse模型输入的采样点就是正常的采样点，之后模型会输出体积密度，我们利用体积密度计算一个权重，然后在这个方向上根据权重去采样n_importance个点，输入到coarse模型中去训练。这样有个好处就是虽然我不知道哪些点有用和哪些点没用，那么我们开始全都采一下，训练一个coarse模型(注意coarse和fine是同时训练的)，之后从coarse模型的体积密度就可以看出来哪些是有用的点，哪些是没用的点，然后根据体积密度计算权重之后归一化，再去之前采样的点最中间的一个根据归一化后的权重采样点，那么这些点就是我们认为有用的点，使用这些点训练fine模型。

至此NeRF的公式推导和原理就到此结束了，上述理解和公式推导我也是参考别人写的理解之后自己总结归纳出来的，相关的参考文献和参考链接我会放到文章末尾。最后简单看一眼作者的消融实验，这里VD是(View Dependence)，如果没有VD就是输入不含有视角信息。我们发现视角信息、位置编码还是比较重要的，分层采样相对而言不如视角信息和位置编码重要。

Q.E.D.

馆主君晓

NeRF-用于视角合成的神经辐射场

相关背景

文章解读

整体介绍

公式推导和原理分析

Urban NeRF

馆主君晓